Research topics:

Quantum Communication
Quantum Teleportation
Exploiting the Similarities of Quantum and Optical Systems
Quantum Information Processing with Classical Light
Quantum Measurement and Control
Measurement-Based Feedback Control
Control of Quantum Systems by Quantum Systems
Quantum Computing to solve Optimisation Tasks
Quantum Computing Verification and Validation

Quantum Communication

Storing and processing information in individual quantum systems promises unprecedented computational power and communication security. Future computing technology is anticipated to be partly based on the ability to manipulate individual atoms, nuclear spins or light particles (photons) in quantum computers. Encoding information in single photons, the elementary building blocks of light, allows for the possibility to communicate securely. Any attempt to read out the information from the individual photons is very likely to be detected because of the disturbance caused by such interventions.

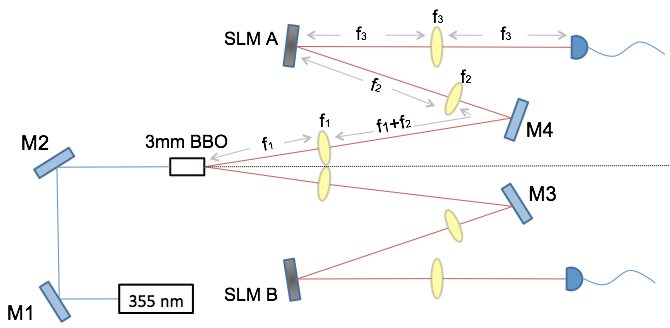
Above: A laser pumping a non-linear crystal produces pairs of single photons which are entangled and can be used as resource for small quantum computing tasks, quantum cryptography or quantum teleportation. By means of spatial light modulators (SLMs) information can be encoded in the single photons. The SLMs are made from programmable liquid crystal displays (LCDs).

In close collaboration with the Structured Light Lab at the University of Witwatersrand in Johannesburg, the research group of Prof Konrad is studying the possibilities of quantum information processing and communication with light. Our vision is to help to develop the technical means for a global quantum network that can be used to transmit quantum information between quantum computing nodes or to send information secure against eavesdropping.

Currently our research is focused on encoding information in particular light modes so called Laguerre-Gauss (LG) modes that have corkscrew-like wave fronts and carry orbital angular momentum. Compared to the polarisation of photons, spatial light modes have a much higher storage capacity: A single photon can store only a basic unit of quantum information - one qubit- in its polarisation but nearly a higher number of qubits in superpositions of different spatial light modes. So far our studies with photons comprise three areas: a) Encoding and processing of information and quantum correlations (entanglement) in LG modes, b) Study of information loss in transmission channels due to turbulence and c) quantum teleportation with spatial light modes.

Quantum Teleportation

In classical physics it is possible, in principle, to detect the state of a single system, for example the position and momentum of a point particle, transmit the information about that state to a remote location and then reconstruct it within a second system. This principle of “classical teleportation” underlies telecommunication techniques such as the transfer of documents via facsimile. Quantum physics, however, excludes the possibility to detect or duplicate the state of a single microscopic system and thus rules out all forms of classical teleportation with atoms, photons or other quantum systems. It is thus surprising, that the state transfer between quantum systems can nevertheless be realized according to the rules of quantum physics by means of “quantum teleportation”. This procedure makes use of quantum correlations between quantum systems – entanglement- which is stronger than the usual correlations between classical particles.

Quantum teleportation lies at the core of quantum communication which is the quantum analog of telecommunication, and can also be employed to enhance the success probability in quantum computing with photons. Moreover, it is one of the crucial ingredients for enabling long-distance quantum cryptography - a technique to transmit information secure against eavesdropping.

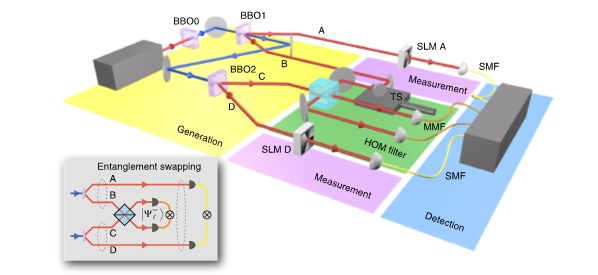
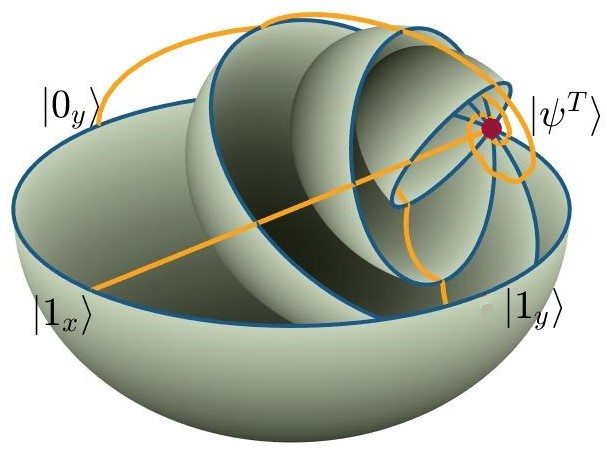
The teleportation of the state of a photon in arm B that is entangled with a photon in arm A by means of an entangled pair in arms C and D produces entanglement between remote photons A and D that never interacted. Since here entanglement of photon pairs in A B and C D is swapped to entanglement between pairs in AD and BC, this process is knows as entanglement swapping. The concept and theory for this experiment conducted by Jonathan Leach’s group in Scotland was jointly worked out by Andrew Forbes (Wits), Jonathan Leach (Heriot Watt), Stef Roux (NMISA) and Thomas Konrad (UKZN).

Exploiting the Similarities of Quantum and Optical Systems

Just like quantum systems, laser light can be superimposed, interferes and even shows a form of entanglement between its polarisation, frequency, and spatial degrees of freedom. This suggests to use so-called classical light to assist quantum mechanical applications.

For example, it is possible to detect the distortions of a single photon due to atmospheric turbulence by means of a co-propagating laser beam and correct them. On the other hand, methods known for quantum systems can also be applied to optics. For example, entanglement measures can be used to determine the ability of intense vector laser beams to cut through metals.

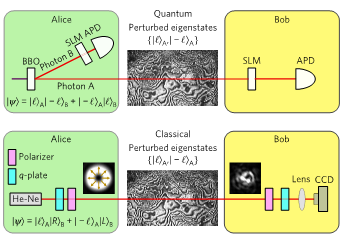
Images from coauthored article in Nature Physics 13, 397 2017: The phase distortion of an electromagnetic wave due to turbulence is identical for a single photon (above) and laser light (below). A tomography of the channel can be realised in a single shot experiment using classical entanglement between polarisation and spatial modes in the laser beam. The information about the channel can be used for error-correction, as shown below in a transmitted picture of James Clerk Maxwell before (left) and after (right) error correction.

Quantum Information Processing with Classical Light

The Konrad group is studying the possibilities to realise quantum algorithms using bright laser light. In order to beat the best existing computers, for example by calculating the factors of a large number faster, a quantum computer would need approximately 10 000 qubits. Currently, quantum registers with only up to 70 qubits are available. In this situation, we are searching for optical implementations. So far, we have designed optical solutions for some algorithms: the Deutsch, Deutsch-Josza, and the Grover algorithm.

Optical realisation of a Grover search of an unstructured database by means of lenses and phases plates. The number 42 is marked by a phase shift which is converted into an amplitude amplification in the output beam.

Remarkably, it turns out that efficient preparation, logic transformations and read out appears possible to realise with classical light. For example, we realised the core operation of the Grover algorithm, a “reflection about the zero” in a single step without a spatial interferometer using LG modes of light. However, the capacity of the information storage in classical light seems limited by the wavelength and the size of the light field. We are currently investigating whether there exist solutions to the storage issue in terms of superoscillations and superresolutions.

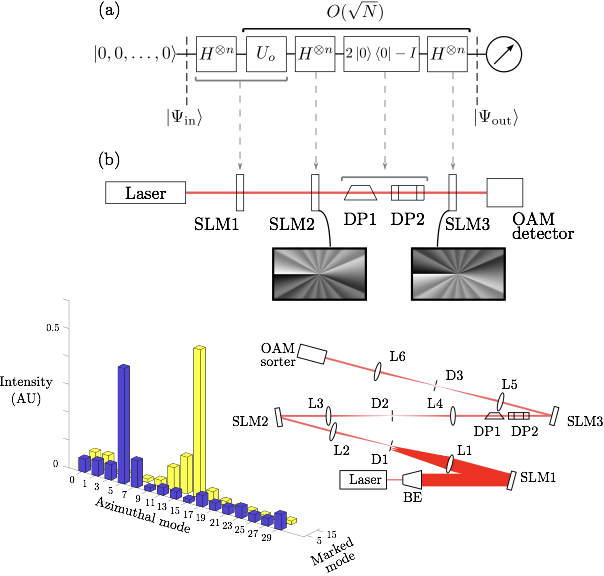
Optical realisation of a Grover search using Orbital Angular Momentum (OAM). Top: (a) Shows the quantum circuit for the Grover algorithm. represents the Hadamard gate and is the oracle. (b) Represents the optical translation of the quantum circuit depicted above. The insets show the phase modulation required to perform the Hadamard and the inverse Hadamard transformation. Bottom right: Experimental scheme. SLM: Spatial Light Modulator; DP: Dove Prism and OAM detector: Mode sorter. Bottom left: Modal decomposition for a database of eight elements. A different mode was marked in each run. We observe that the mode of the output superposition with the highest intensity indicates the mode marked by the oracle.

Quantum Measurement and Control

Quantum control is considered much more difficult than the control of classical systems. This is not only due to the susceptibility of atoms and electrons to tiny disturbances because of their lack of inertia, but also implied by the fundamental properties such as Heisenberg’s uncertainty, that forbids a quantum particle to be prepared with a precise position and momentum simultaneously. Moreover, high resolution measurements lead to drastic state changes. For example, a sharp measurement of the position of a particle would collapse the support of the wave function to single point. In order to monitor the wave function of particles, unsharp indirect measurements can be used that induce weak state change but also offer little information gain. However, a sequence of such measurements can lead to faithful monitoring of the wave function, if its natural dynamics dominate the weak disturbances due to the measurements.

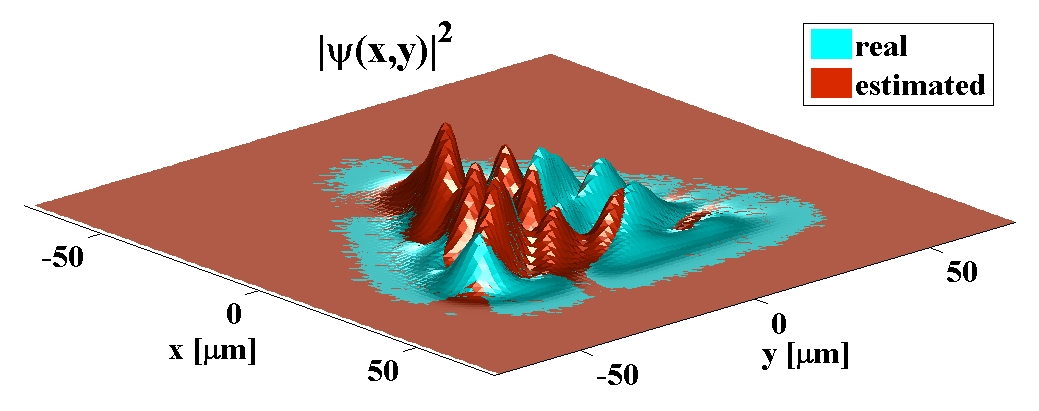
A snapshot from the video featured at the top of the page created by computer simulation carried out by Andreas Rothe, a former MSc student in the Konrad group. The monitored wavefunction (green) of a particle moving is in a chaotic Heinon Heiles potential and its estimate (brown) is based on continuous weak measurement.

In spite of the sensitivity of tiny quantum systems, such as single trapped ions, against external influences, e.g. measurements, or possibly just because of this sensitivity, we found methods to completely control the quantum state under certain conditions.

Measurement-Based Feedback Control

Based on unsharp measurements augmented with feedback a quantum system can be driven in targeted dynamics, protected against noise etc. For this purpose, we developed a method together with Hermann Uys (former Stellenbosch University now IONQ) called quantum control through “Self-fulfilling Prophecy”, which is explained in the diagramme below at the simple example of a two-level quantum system.

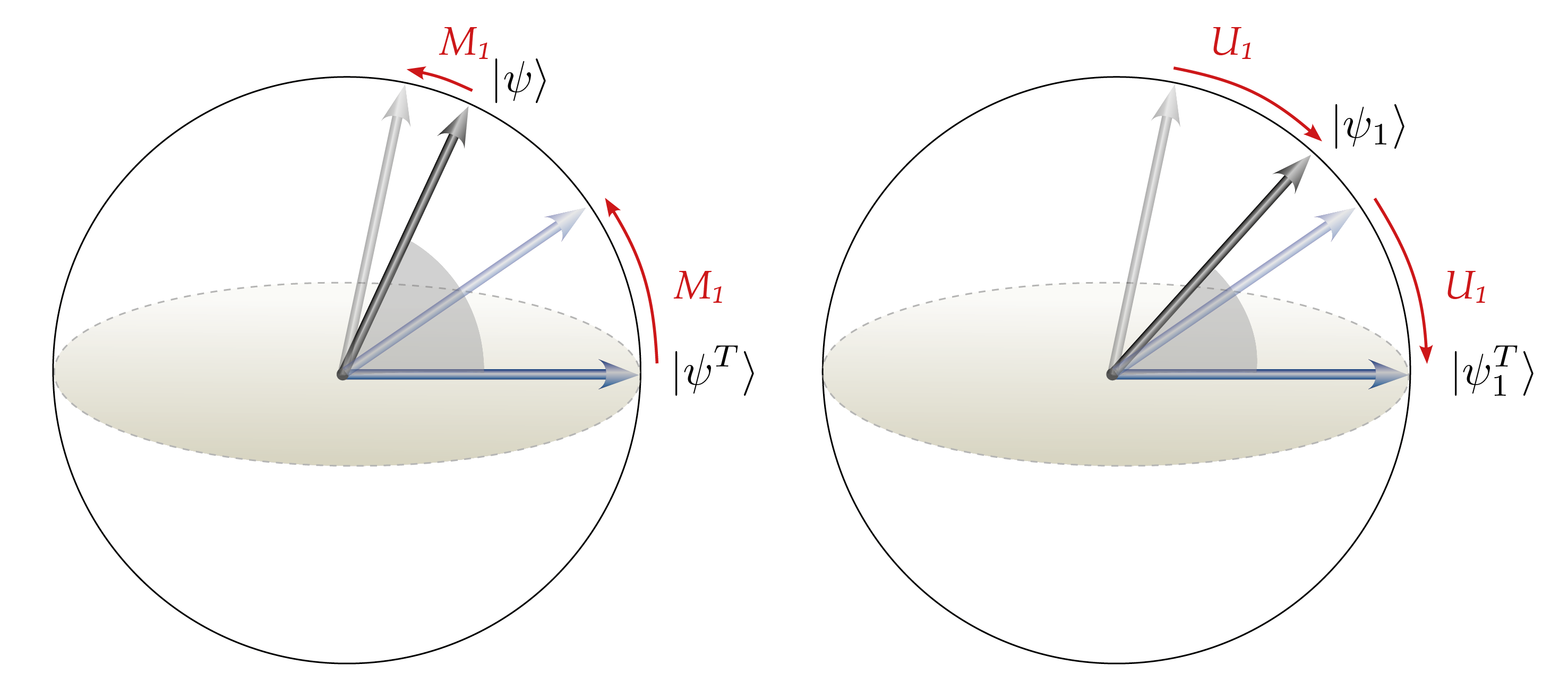
The energy of a trapped ion in a superposition of two energy states (corresponding to the north and south pole) is measured. Due to the unsharp measurement the initial state moves towards one of the energy states. The diagramme on the left shows the situation that two possible initial states move towards the north pole. Assuming that the system starts in the state on the equator of the sphere, a feedback operation returns it to its initial position (left diagramme). If the system were instead initially in a state further north it would end after the feedback closer to the equatorial state. In fact, after a number of measurement feedback cycles an arbitrary initial superposition state can be transferred into any target state using appropriate feedback.

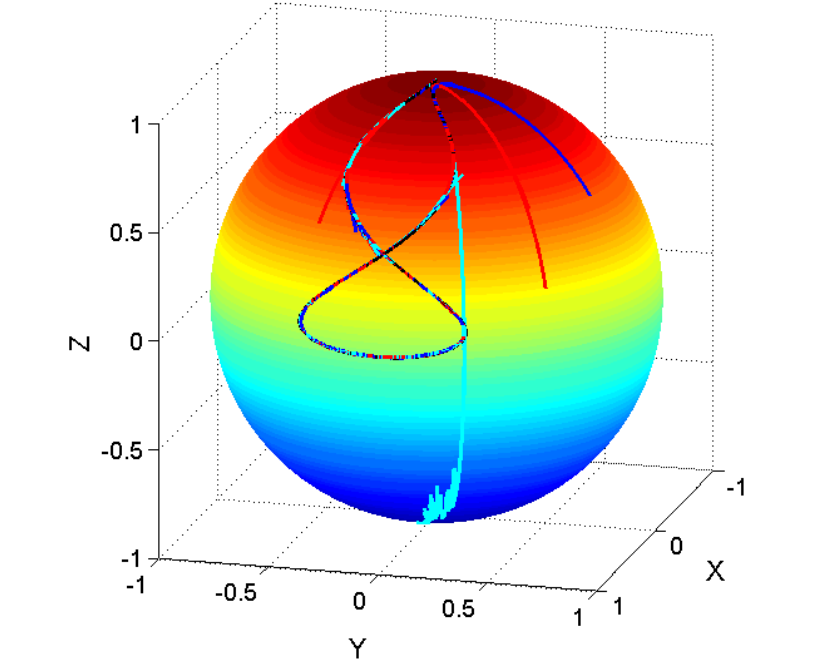
Using this method the system can be driven from any initial state (see different trajectories) into dynamics on certain timescales.

Quantum Systems controlled by Quantum Systems

In our collaboration, Hermann Uys (IONQ) asked the question whether quantum systems could be controlled by other quantum systems. Our interpretation of quantum controllers is illustrated in the picture (produced by artist Pamela Benporath). A quantum (controller system interacts with the target system, senses its state properties and changes them in order to drive it towards an target state. In a sequence of such interactions with a multitude of quantum controllers, the system is driven into a target state or even target dynamics. The information about the target state is encoded either in the interaction (Hamiltonian) or in the state of the quantum controllers, which could be the result of a quantum computation.

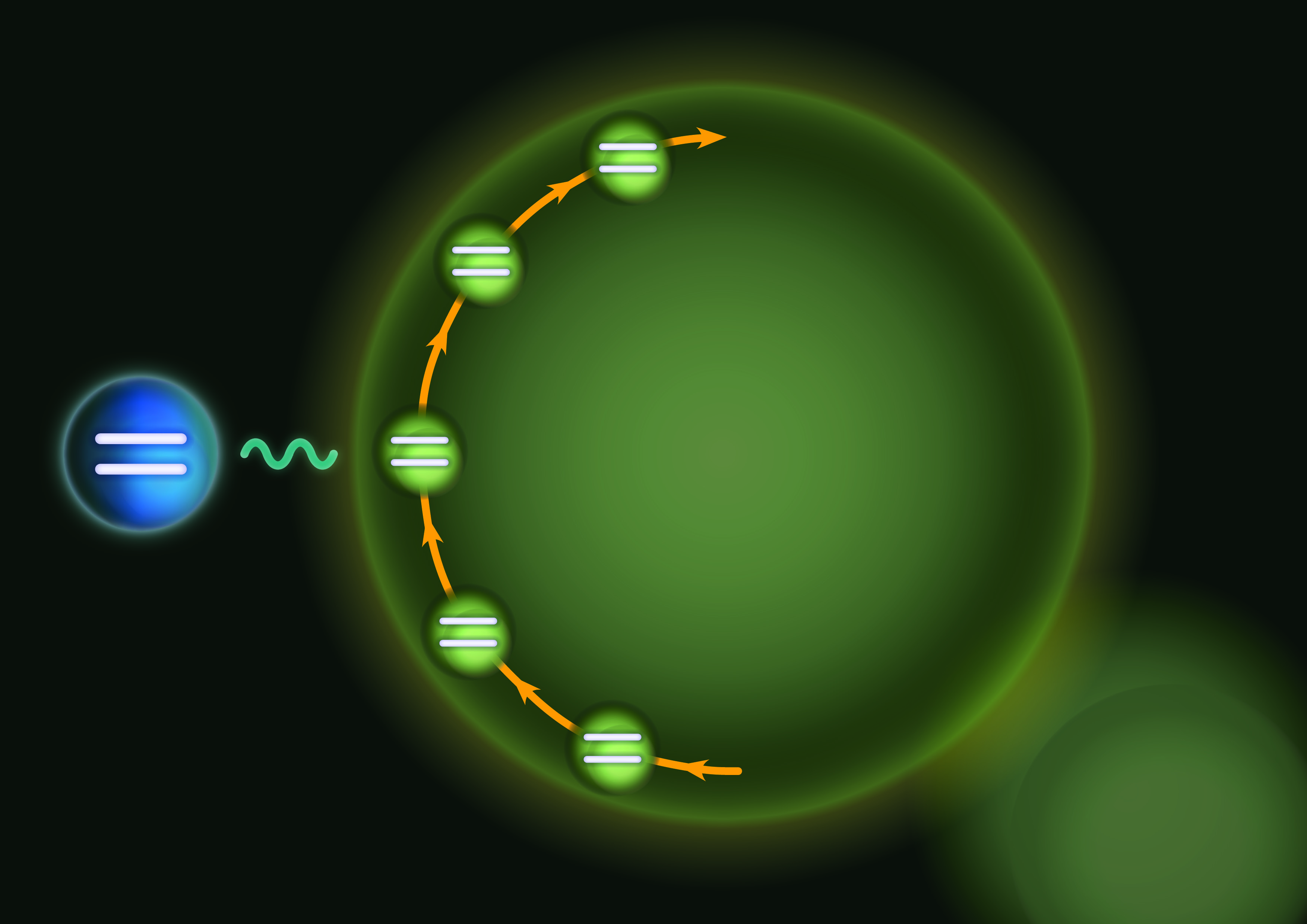
A target system (two level atom on the left) couples sequentially to quantum controllers (two level atoms on the right). The resulting entanglement with controllers is displaced in subsequent interactions until the target atom ends in a pure target state.

This opens the possibility to directly control quantum systems without using measurements which translate quantum information into classical information. One could say, the control thus takes place in the quantum realm without taking a deviation via the classical realm. A particular advantage would be that the target states could be the result of quantum computations. One can speculate whether such quantum computations of target states could lead to new speed ups since the answer of a quantum computation is given in terms of quantum information while transformation into classical information need additional steps.

Such a kind of control has been first described by Seth Lloyld from the MIT [S.Lloyd, “Coherent quantum feedback,” Phys. Rev. A 62, 022108 (2000)] and is known as coherent feedback control as opposed to measurement-based feedback control. For our control by a interaction with a sequence of quantum controllers we proved convergence theorem, and designed various control schemes for quantum systems with finite dimensional state space.

In this control scheme, which is based on partial state swaps with the controllers, the consecutive interactions with the quantum controllers rotate and contract the sphere of all states of the system into the point that represents the target state (red).

Quantum Computing to solve Optimisation Tasks

Optimisation is omnipresent in science, economy and industry. For example in industry, costs and sustainability depend on the optimisation of production, storage and transport. Computing the optimal parameters for complex processes is exponentially hard, i.e. it requires as function of input size exponentially growing computational time or register size on classical computers.

However, there might exist algorithms for quantum computers that could solve such optimisation tasks efficiently (with polynomially growing resources). A practical challenge is that existing quantum computers are noisy, intermediate scale quantum (NISQ) devices, that make it difficult to gain a quantum advantage.

We are looking to solve optimisation problems on existing quantum computers encoding information in the amplitudes of quantum states. Since the state of a quantum computer with 50 quantum bits (a qubit is the basis unit of quantum information that can be stored in a quantum system with two basis states) is determined by a total of 2 to the power 50 basis states, it can thus store the same number of amplitudes. This corresponds to the values of 10 to the power 15 variables that can be processed in parallel. However, the main problem is how to read in the input values and read out results. The QIGK is researching quantum optimisation algorithms and solutions to the input-output problem.

Quantum Verification and Validation

Background of Verification and Validation (V&V)

Verification and validation serve to evaluate products, services and systems as diverse as pharmaceuticals, medical devices, buildings and roads, financial accounting or health care. Verification asks whether the system was build according to specifications (“Was the thing built right?”) and validation addresses the question whether the system serves its purpose (“Was the right thing built?). Among the most important applications is the verification and validation of computer simulations [1].

With sufficient computational power, a designed system can be improved by simulating its properties, for example the aerodynamics of a new jet plane, on a computer instead of building, testing and re-engineering it. However, this shortcut requires accurate modeling of the system and its environment. For this purpose, the task of V&V is essential: to make sure the computer simulation reflects the model (verification) and the model reflects reality (validation) with high fidelity. Computer simulations enable also testing under extreme conditions and in accident scenarios, where experiments are not possible or too costly.

Foundations of V&V for simulation software have been developed in nuclear reactor safety as well as in nuclear waste storage communities and, in general, in the field of computational fluid dynamics, which coined a lot of the terminology, discovered methods and invented processes [2]. An important aspect of V&V is the generation of benchmarks that allow to test the accuracy and reliability of a system. For computer simulations, a benchmark could be the comparison of the outputs to an analytic or highly accurate numerical solution for a special case under simplifying assumptions. Depending on the complexity of the system, V&V can take up to 50% of the total development costs.

In some cases verification of code cannot even be achieved using classical computers in reasonable time. For example, the US based company Lockheed Martin developed software for aircrafts to automate evasive maneuvers to escape from danger. Because of the complexity of the software and the aerodynamics involved, conventional computers do not have the capacity to verify and validate the flight control software [3]. In this case V&V might be facilitated in future using quantum computers with registers of several millions of physical qubits (“quantum bits”, the analog of “bits” in a conventional computer). Optimistic predictions reckon that such large-scale quantum computers (QC) with error correction might be available in ten to twenty years time. However, reliable predictions about the advent of QC cannot be made at this point [4].

There are software engineering institutes that are working on V&V for flight control software using a Quantum Approximation Optimisation Algorithm with contemporary QCs, which have typically 50 qubits [5]. This class of quantum computers is known as Noisy Intermediate Size Quantum (NISQ) computers. As noted in the progress report [7] on page 160 there are at present promising research directions but no known algorithms or applications that could make effective use of NISQ computers.

An interesting problem for V&V is posed by the advantage of quantum computers – if they are built – to solve problems that are intractable by classical computers. This basically could mean that it is impossible to verify the solutions by classical means. A certain class of computational problems (NP) has solutions that can be checked in reasonable time and with reasonable resources. For example, when the prime factors of a large integer number are found by a quantum computer (Shor Algorithm), one can efficiently multiply them on a classical computer to check the result. However, the class of problems that can be solved by a quantum computer efficiently (BQP) is presumably much bigger than NP. Therefore, once quantum software can be run, the problem how to do quantum V&V becomes important.

An issue for V&V of quantum technology in general is the complexity of quantum systems. For example, the number of steps for verification and validation of preparation procedures of quantum states by so called state tomography increases exponentially with the system size (number of qubits involved). The same is true for V&V of state transformations and measurements. In other words, most parts of real world quantum devices are difficult to test. For this reason quantum technology has sprouted a new branch developing quantum V&V [6].

Summary

Verification and validation of complex systems is a challenging and necessary requirement in various fields calling for a new computational paradigm. Quantum computing on large-scale quantum computers, if they are developed, might enable V&V of conventional complex systems and software. On the other hand, quantum technology and, in particular, quantum computers require a new kind of V&V which is in the following referred to as quantum V&V.

How does Quantum V&V work

V&V of Quantum Devices in general

Usually it takes exponentially many measurements to verify a preparation procedure of the state of a quantum system. However, the task is only to check whether the target fidelity of state preparation is sufficiently high. This can be accomplished by a measurement of an observable that witnesses the proximity to a target state of the preparation device – a so-called fidelity witness [7].

To verify a device that transforms quantum states, the same concept can be applied using the duality between states and channels. Each quantum channel (state transformer) corresponds to a particular state, which is obtained when the channel acts on a system that is maximally entangled with a partner system. A verification of a transformation device can thus be obtained by applying the device to a system that is entangled with a partner system and measuring a fidelity witness on the system pair. There are other more efficient measurements to verify channels [8].

Similarly, measurement instruments can be tested using certified preparation procedures. However, there are more advanced techniques based on self-testing by means of quantum random access codes [9].

Any quantum device consists of a preparation, transformation and a measurement stage, which could be verified in principle separately using the techniques mentioned above. On the other hand, often the results of V&V can be employed to improve the design of the tested device. For this purpose, more information to analyse errors or noise is desirable [12]. For example, a technique known as gate-set tomography, to analyse logic gates of quantum computers, which does not rely on pre-verified preparations or measurements, has been successfully used to improve the quality of qubits in a quantum computer based on trapped ions [10].

V&V of Quantum Computers

Although applicable to all quantum devices, quantum computers need V&V particularly, because of their high complexity, generating output that cannot be simulated with classical computers. In principle, any quantum algorithm that solves a computational problem efficiently (element of the class BQP) can be verified by so-called interactive protocols. In such a protocol, there is a verifier (Arthur) and at least one prover (Merlin). Merlin has a quantum computer that can solve BQP problems. Arthur requires some amount of quantum computational power independent of the size of the algorithm. At least he needs to be able to prepare or measure single qubit systems carrying quantum information that is communicated and processed in Merlin’s quantum computer according to Arthur’s instructions.

There are various interactive protocols, most of them use blind computing, i.e. the computer to be verified, cannot distinguish its quantum input nor the problem it is solving. This is enabled by cryptographically encoding the input as well as the instructions, the output can be decoded later. The procedure serves the purpose to hide the actual test from the server Merlin in order to prevent cheating. The principle of independent verification and validation follows the principle of independent and objective review.

Summary

Quantum V&V is a recent but fast developing and essential branch of quantum technology. It offers new methods that require little quantum computational power to verify efficient quantum algorithms running on quantum computers. Useful applications on NISQ computers and their benchmarks have to still be developed.

Quantum V&V a new Emerging Market?

Because of the complexity of quantum systems, quantum technology requires for its development V&V. Moreover, especially the information security of cryptographic applications of quantum technology, such as quantum key distribution and blind quantum computing, has to be certified independently from the producer. Since quantum computers solve problems with solutions that cannot be easily checked on a classical computer, V&V is here of particular importance. QT will thus automatically produce a market for its newly developing branch of verification and validation of quantum devices and their parts. The size of this market will depend on the size of the market for quantum technology itself.

Taking into account conservative cost estimates of V&V between 10% and 35% of the development costs of conventional complex devices and software [11], it is a reasonable and conservative assumption that the costs of quantum V&V might also amount to 1/10 to 1/3 of the development costs for quantum devices with an additional market for certification of quantum devices. With an estimated total market size for QC of 50 billion US $ a year, a V&V market of 5 to 15 billion US $ a year seems reasonable. Here, it is assumed that the costs for the production of a quantum device and its verification follow the same ratio as the respective development costs.

There is already a Canadian company, Quantum Benchmark, [12] that offers service and software for performance validation of quantum computers, error analysis and error mitigation to users and producers of quantum computers.

The US department of defense recognized the need for quantum V&V and issued in 2018 a detailed call for related projects [13].

Summary

A market for Quantum Technology will produce a market for quantum V&V. Quantum Benchmark is the first company that offers quantum V&V as a service and in form of software.

Quantum V&V activities in the QIGK

Our activities are financially supported by grants from the South African Quantum Technology Initiative. In particular, we can offer bursaries for 1 MSc, 1 PhD and two postdoctoral fellows. We focus on the following research fields

1. V&V of Quantum Communication devices

2. V&V of Quantum Computers

Add 1) In terms of Quantum Communication devices we have been collaborating with the National Metrology Institute of South Africa at the CSIR in Pretoria. Our goal is to check Quantum Cryptography Devices, but also components that can be used for a quantum communication network such as teleportation devices, sources of entanglement, photo-detectors, coincidence detectors etc. Currently we are designing a device to verify and validate based on the Hong-Ou-Mandel effect sources of entangled photon pairs.

Add 2) We are interested in the verification of universal quantum computers. We have analysed the benchmarking for the Google sycamore quantum processor and written a comment on the related quantum supremacy claim [14]. Based on what we learned from this, we are studying a new method that we designed to verify and validate universal quantum computers, using statistics of outputs from applying random quantum gates. This method can be used for quantum computers with a certain size without relying on additional calculations of classical supercomputers as the original method [15].

A different approach is investigated by QIGK based on an interactive protocol and blind quantum computation. Here Arthur sends quantum information to Merlin or encrypted instructions that produce certain outputs deterministically that are unknown to Merlin. Checking the output statistics enables then Verification and validation.

References

[1] Oberkampf, William L., & Trucano, Timothy G. (2008). Verification and validation benchmarks. Nuclear Engineering and Design, 238(3), 716-743. doi:101016/jnucengdes200702032

[2] Roache, P .J., Verification and Validation in Computational Science and Engineering. 1998, Albuquerque, NM: Hermosa Publishers.

[3] Carnegie Mellon University Software Engineering Institute Research Review 2019, p. 37. https://resources.sei.cmu.edu/asset_files/Brochure/2019_015_001_635740.pdf

[4] National Academies of Sciences, Engineering, and Medicine 2019. Quantum Computing: Progress and Prospects. Washington, DC: The National Academies Press. https://doi.org/10.17226/25196., p.157.

[5] Gheorghiu, A., Kapourniotis, T. & Kashefi, E. Verification of Quantum Computation: An Overview of Existing Approaches. Theory Comput Syst 63, 715–808 (2019). https://doi.org/10.1007/s00224-018-9872-

[6] Aolita, L., Gogolin, C., Kliesch, M. et al. Reliable quantum certification of photonic state preparations. Nat Commun 6, 8498 (2015). https://doi.org/10.1038/ncomms9498

[7] Wu, Ya-Dong and Sanders, B.C., Efficient verification of bosonic quantum channels via benchmarking, 2019 New J. Phys. 21 073026.

[8] Karthik Mohan et al 2019 New J. Phys. 21 083034.

[9] Erhard, A., Wallman, J.J., Postler, L. et al. Characterizing large-scale quantum computers via cycle benchmarking. Nat Commun 10, 5347 (2019). https://doi.org/10.1038/s41467-019-13068-7

[10] Blume-Kohout, R., Gamble, J., Nielsen, E. et al. Demonstration of qubit operations below a rigorous fault tolerance threshold with gate set tomography. Nat Commun 8, 14485 (2017). https://doi.org/10.1038/ncomms14485

[11] Andra ́s Pataricza et al. Cost Estimation for Independent Systems Verification and Validation in Certifications of Critical Systems - The CECRIS Experience, eds Andrea Bondavalli, Francesco Brancati , ‪River Publishers, 30 Nov 2017 - Technology & Engineering - 314 pages‬

[12] Quantum Benchmark Webpage https://quantumbenchmark.com/about-us/

[13] Funding Tool Details: Software Tools for Scalable Quantum Validation and Verification https://www.sbir.gov/sbirsearch/detail/1482265

[14] Anirudh Segireddy , Benjamin Perez-Garcia , Adenilton da Silva, “Comment on the Quantum Supremacy Claim by Google”, considered but rejected by Nature, to be resubmitted elsewhere, arXiv.org:2108.13862.

[15] F. Arute, K. Arya, R Babbush et al., “Quantum Supremacy using a programmable superconducting processor,” Nature 574, 505–510 (2019).